Вернуться к оглавлению
Экстримальные задачи непрерывного типа.
Устловие:
Считая, что все переменные являются положительными величинами, найти оптимальное решение симплекс-методом линейного
программирования приведенных ниже задач (предполагается, что все переменные не отрицательны).
Задание.
L(x)=-16x1-x2+x3+5x4+5x5
2x1+x2+x3=10
-2x1+3x2-x4=6
2x1+4x2-x5=8
Решение.
L(x) ->min (2 к/р)
L(x) ->max (3 к/р)
1. Нахождение минимума функции L(X):
Так как нет базиса в 3-ем уравнение добавляем еще одну вспомогательную переменную x6
2x1+x2+x3=10
-2x1+3x2-x4=6
2x1+4x2-x5+x6=8 x6->min
L(x)->min
Найдем опорное решение с помощью вспомогательной задачи Данцига (метод искусственного базиса):
Lвсп=x6->min
Нахождение опорного решения:
2x1+x2+x3=10
-2x1+3x2-x4=6
2x1+4x2-x5+x6=8
Lвсп=x6->min
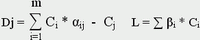
Составим симплекс таблицу*:
Таблица1.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
10 |
0 |
2 |
1 |
1 |
0 |
0 |
0 |
10 |
| x4 |
6 |
0 |
-2 |
3 |
0 |
1 |
0 |
0 |
2 |
| x6 |
8 |
1 |
2 |
4 |
0 |
0 |
-1 |
1 |
2 |
| Lвсп= 8 |
Dj |
2 |
4 |
0 |
0 |
-1 |
0 |
|
Таблица2.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
8 |
0 |
1.5 |
0 |
1 |
0 |
0.25 |
-0.25 |
|
| x4 |
0 |
0 |
-3.5 |
0 |
0 |
1 |
0.75 |
-0.75 |
|
| x2 |
2 |
0 |
0.5 |
1 |
0 |
0 |
-0.25 |
0.25 |
|
| Lвсп= 0 |
Dj |
0 |
0 |
0 |
0 |
0 |
-1 |
|
Все маргиналы меньше или равны нулю. Оптимизация прошла успешно.
Lвсп= 0 => Xопор=(0,2,8,0,0)T
Найдем минимум функции L(x) с помощью симплекс-метода. Составим симплекс таблицу:
Таблица3.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| -16 |
-1 |
1 |
5 |
5 |
|
Bi/aij
|
| x3 |
8 |
1 |
1.5 |
0 |
1 |
0 |
0.25 |
|
| x4 |
0 |
5 |
-3.5 |
0 |
0 |
1 |
0.75 |
|
| x2 |
2 |
-1 |
0.5 |
1 |
0 |
0 |
-0.25 |
|
| L= 6 |
Dj |
-0.5 |
0 |
0 |
0 |
-0.75 |
|
Все маргиналы меньше или равны нулю. Оптимизация прошла успешно.
Lmin= 6
X=(0,2,8,0,0)T
2. Нахождение максимума функции L(X):
L(x)=-16x1-x2+x3+5x4+5x5->max
Или: L(x)=16x1+x2-x3-5x4-5x5->min
Ограничения:
2x1+x2+x3=10
-2x1+3x2-x4=6
2x1+4x2-x5=8
Так как ограничения не изменились, то и опорное решение останется прежним:
Xопор=(0,2,8,0,0)T
Составим симплекс таблицу:
Таблица4.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| 16 |
1 |
-1 |
-5 |
-5 |
|
Bi/aij
|
| x3 |
8 |
-1 |
1.5 |
0 |
1 |
0 |
0.25 |
32 |
| x4 |
0 |
-5 |
-3.5 |
0 |
0 |
1 |
0.75 |
0 |
| x2 |
2 |
1 |
0.5 |
1 |
0 |
0 |
-0.25 |
|
| L= -6 |
Dj |
0.5 |
0 |
0 |
0 |
0.75 |
|
Таблица5.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| 16 |
1 |
-1 |
-5 |
-5 |
|
Bi/aij
|
| x3 |
8 |
-1 |
2/3 |
0 |
1 |
-1/3 |
0 |
3/4 |
| x5 |
0 |
-5 |
14/3 |
0 |
0 |
4/3 |
-1 |
0 |
| x2 |
2 |
1 |
-2/3 |
1 |
0 |
-1/3 |
0 |
|
| L= -6 |
Dj |
4 |
0 |
0 |
-1 |
0 |
|
Таблица6.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| 16 |
1 |
-1 |
-5 |
-5 |
|
Bi/aij
|
| x1 |
3 |
16 |
1 |
0 |
0.375 |
-0.125 |
0 |
|
| x5 |
14 |
-5 |
0 |
0 |
1.75 |
0.75 |
1 |
|
| x2 |
4 |
1 |
0 |
1 |
0.25 |
0.25 |
0 |
|
| L= -18 |
Dj |
0 |
0 |
-1.5 |
-0.5 |
0 |
|
Все маргиналы меньше или равны нулю.
Оптимизация успешно завершена.
Найдено оптимальное решение:
X*=(3,4,0,0,14)T
Lmax=18.
Ответ:
Минимум:
X*=(0,2,8,0,0)T
Lmin= 6
Максимум:
X*=(3,4,0,0,14)T
Lmax=18.
|


