Вернуться к оглавлению
Экстримальные задачи непрерывного типа.
Устловие:
Считая, что все переменные являются положительными величинами, найти оптимальное решение симплекс-методом линейного программирования приведенных ниже задач (предполагается, что все переменные не отрицательны).
Задание.
L(x)=2x1+x2-x3+x4-x5
x1+x2+x3=5
2x1+x2+x4=9
x1+2x2+x5=7
Решение.
Поиск min. L(x)->min.
Уравнения уже записаны в каноническом виде.
Начинаем решение основной задачи.
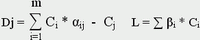
Таблица1.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| 2 |
1 |
-1 |
1 |
-1 |
|
Bi/aij
|
| x3 |
5 |
-1 |
1 |
1 |
1 |
0 |
0 |
|
| x4 |
9 |
1 |
2 |
1 |
0 |
1 |
0 |
|
| x5 |
7 |
-1 |
1 |
2 |
0 |
0 |
1 |
|
| L= -3 |
Dj |
-2 |
-3 |
0 |
0 |
0 |
|
Все маргиналы меньше или равны нулю.
Оптимизация успешно завершена.
Найдено оптимальное решение:
Минимум:
X*=(0,0,5,9,7)T
L*= -3.
Найдем максимум: max(L(x))=-min(-(L(x)).
Таблица2.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| -2 |
-1 |
1 |
-1 |
1 |
|
Bi/aij |
| x3 |
5 |
1 |
1 |
1 |
1 |
0 |
0 |
5 |
| x4 |
9 |
-1 |
2 |
1 |
0 |
1 |
0 |
9 |
| x5 |
7 |
1 |
1 |
2 |
0 |
0 |
1 |
3.5 |
| L= 3 |
Dj |
2 |
3 |
0 |
0 |
0 |
|
X2 сделаем базисом, т.к. Dj в этом столбце максимально.
min(Bi/aij)={5,9,3.5}=3.5
3 Строку умножим на 0.5
К 1-ой строке прибавим -0.5 строки 3.
К 2-ой строке прибавим -0.5 строки 3.
Таблица3.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| -2 |
-1 |
1 |
-1 |
1 |
|
Bi/aij |
| x3 |
1.5 |
1 |
0.5 |
0 |
1 |
0 |
-0.5 |
3 |
| x4 |
5.5 |
-1 |
1.5 |
0 |
0 |
1 |
-0.5 |
3.667 |
| x2 |
3.5 |
-1 |
0.5 |
1 |
0 |
0 |
0.5 |
7 |
| L= -7.5 |
Dj |
0.5 |
0 |
0 |
0 |
-1.5 |
|
X1 сделаем базисом, т.к. Dj в этом столбце максимально.
min(Bi/aij)={3,3.667,7}=3
1 Строку умножим на 2
К 2-ой строке прибавим -3 строки 1.
К 3-ой строке прибавим -1 строки 1.
Таблица4.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
| -2 |
-1 |
1 |
-1 |
1 |
|
Bi/aij |
| x1 |
3 |
-2 |
1 |
0 |
2 |
0 |
-1 |
|
| x4 |
1 |
-1 |
0 |
0 |
-3 |
1 |
1 |
|
| x2 |
2 |
-1 |
0 |
1 |
-1 |
0 |
1 |
|
| L= -9 |
Dj |
0 |
0 |
-1 |
0 |
-1 |
|
Все маргиналы меньше или равны нулю.
Оптимизация успешно завершена.
Найдено оптимальное решение:
Максимум:
X*=(3,2,0,1,0)T
L*= 9.
Ответ:
Минимум:
X*=(0,0,5,9,7)T
L*= -3.
Максимум:
X*=(3,2,0,1,0)T
L*= 9.
|


