Вернуться к оглавлению>>
Экстримальные задачи непрерывного типа.
Устловие:
Считая, что все переменные являются положительными величинами, найти оптимальное
решение симплекс-методом линейного программирования приведенных ниже задач
(предполагается, что все переменные не отрицательны).
Задание.
L(x)=2x1-x2-x4
x1-2x2+x3=10
2x1+x2+2x4>=18
3x1+2x2+x4<=36
Решение.
Приведем к каноническому виду:
x1-2x2+x3=10
2x1+x2+2x4-x5=18
3x1+2x2+x4+x6=36
Т.к. во-втором ограничение нет базиса, то введем ещё одну переменную
x7. Найдем начальный базис по методу вспомогательной задачи Данцига.
Введем вспомоготельную функцию Lвсп(х)=x7->min.
Решим вспомогательную задачу симплекс методом.
Поиск min. Lвсп(x)->min.
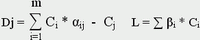
Таблица1.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
0 |
|
| x7 |
18 |
1 |
2 |
1 |
0 |
2 |
-1 |
0 |
1 |
9 |
| x6 |
36 |
0 |
3 |
2 |
0 |
1 |
0 |
1 |
0 |
36 |
| Lвсп= 18 |
Dj |
2 |
1 |
0 |
2 |
-1 |
0 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={9,36}=9
Сделаем стобец x4 базисом.
Для этого прибавим к строке 3 (-0.5) строки 2.
Строку 2 умножим на 0.5.
Таблица2.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
0 |
|
| x4 |
9 |
0 |
1 |
0.5 |
0 |
1 |
-0.5 |
0 |
0.5 |
|
| x6 |
27 |
0 |
2 |
1.5 |
0 |
0 |
0.5 |
1 |
-0.5 |
|
| Lвсп= 0 |
Dj |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
Все маргиналы меньше или равны нулю. Оптимизация прошла успешно.
Поскольку Lвсп= 0 => x7=0.
Xопор=(0,0,10,9,0,27)T
Теперь найдем симплекс методом минимум функции
L(x)=2x1-x2-x4->min при следующих ограничениях:
x1-2x2+x3=10
x1+0.5x2+x4-0.5x5=9
2x1+1.5x2+0.5x6=27
Таблица3.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 2 |
-1 |
0 |
-1 |
0 |
0 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
|
| x4 |
9 |
-1 |
1 |
0.5 |
0 |
1 |
-0.5 |
0 |
18 |
| x6 |
27 |
0 |
2 |
1.5 |
0 |
0 |
0.5 |
1 |
18 |
| L= -9 |
Dj |
-3 |
0.5 |
0 |
0 |
0.5 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={18,18}=18
Сделаем стобец x2 базисом.
К строке 1 прибавим (4) строки 2.
К строке 3 прибавим (-3) строки 2.
Строку 2 умножим на 2.
Таблица4.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 2 |
-1 |
0 |
-1 |
0 |
0 |
|
Bi/aij
|
| x3 |
46 |
0 |
5 |
0 |
1 |
4 |
-2 |
0 |
|
| x2 |
18 |
-1 |
2 |
1 |
0 |
2 |
-1 |
0 |
|
| x6 |
0 |
0 |
-1 |
0 |
0 |
-3 |
2 |
1 |
0 |
| L= -18 |
Dj |
-4 |
0 |
0 |
-1 |
1 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={0}=0
Сделаем стобец x5 базисом.
К строке 1 прибавим строку 3.
К строке 2 прибавим (0.5) строки 3.
Строку 3 умножим на 0.5.
Таблица5.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 2 |
-1 |
0 |
-1 |
0 |
0 |
|
Bi/aij
|
| x3 |
46 |
0 |
4 |
0 |
1 |
1 |
0 |
1 |
46 |
| x2 |
18 |
-1 |
1.5 |
1 |
0 |
0.5 |
0 |
0.5 |
36 |
| x5 |
0 |
0 |
-0.5 |
0 |
0 |
-1.5 |
1 |
0.5 |
|
| L= -18 |
Dj |
-3.5 |
0 |
0 |
0.5 |
0 |
-0.5 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={46,36}=36
Сделаем стобец x4 базисом.
К строке 1 прибавим (-2) строки 2.
К строке 3 прибавим (3) строки 2.
Строку 2 умножим на 2.
Таблица6.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| 2 |
-1 |
0 |
-1 |
0 |
0 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
|
| x4 |
36 |
-1 |
3 |
2 |
0 |
1 |
0 |
1 |
|
| x5 |
54 |
0 |
4 |
3 |
0 |
0 |
1 |
2 |
|
| L= -36 |
Dj |
-5 |
-1 |
0 |
0 |
0 |
-1 |
|
Все маргиналы меньше или равны нулю.
Оптимизация успешно завершена.
Найдено оптимальное решение:
Минимум:
X*=(0,0,10,36)T
L*= -36.
Найдем максимум: max(L(x))=-min(-(L(x)), при следующих ограничениях:
x1-2x2+x3=10
2x1+x2+2x4>=18
3x1+2x2+x4<=36
Решение.
Приведем к каноническому виду:
x1-2x2+x3=10
2x1+x2+2x4-x5=18
3x1+2x2+x4+x6=36
Т.к. во-втором ограничение нет базиса, то введем ещё одну переменную
x7. Найдем начальный базис по методу вспомогательной задачи Данцига.
Введем вспомоготельную функцию Lвсп(х)=x7->min.
Решим вспомогательную задачу симплекс методом.
Таблица7.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
0 |
|
| x7 |
18 |
1 |
2 |
1 |
0 |
2 |
-1 |
0 |
1 |
9 |
| x6 |
36 |
0 |
3 |
2 |
0 |
1 |
0 |
1 |
0 |
36 |
| Lвсп= 18 |
Dj |
2 |
1 |
0 |
2 |
-1 |
0 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={9,36}=9
Сделаем стобец x4 базисом.
Для этого прибавим к строке 3 (-0.5) строки 2.
Строку 2 умножим на 0.5.
Таблица8.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
0 |
|
| x4 |
9 |
0 |
1 |
0.5 |
0 |
1 |
-0.5 |
0 |
0.5 |
|
| x6 |
27 |
0 |
2 |
1.5 |
0 |
0 |
0.5 |
1 |
-0.5 |
|
| Lвсп= 0 |
Dj |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
Все маргиналы меньше или равны нулю. Оптимизация прошла успешно.
Поскольку Lвсп= 0 => x7=0.
Xопор=(0,0,10,9,0,27)T
Теперь найдем симплекс методом максимум функции
L(x)=2x1-x2-x4->max при следующих ограничениях:
x1-2x2+x3=10
x1+0.5x2+x4-0.5x5=9
2x1+1.5x2+0.5x6=27
max(L(x))=-min(-(L(x))
Таблица9.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| -2 |
1 |
0 |
1 |
0 |
0 |
|
Bi/aij
|
| x3 |
10 |
0 |
1 |
-2 |
1 |
0 |
0 |
0 |
10 |
| x4 |
9 |
1 |
1 |
0.5 |
0 |
1 |
-0.5 |
0 |
9 |
| x6 |
27 |
0 |
2 |
1.5 |
0 |
0 |
0.5 |
1 |
13.5 |
| L= 9 |
Dj |
3 |
-0.5 |
0 |
0 |
-0.5 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={10,9,13.5}=9
Сделаем стобец x1 базисом.
К строке 1 прибавим (-1) строки 2.
К строке 3 прибавим (-2) строки 2.
Таблица10.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| -2 |
1 |
0 |
1 |
0 |
0 |
|
Bi/aij
|
| x3 |
1 |
0 |
0 |
-2.5 |
1 |
-1 |
0.5 |
0 |
2 |
| x1 |
9 |
-2 |
1 |
0.5 |
0 |
1 |
-0.5 |
0 |
|
| x6 |
9 |
0 |
0 |
0.5 |
0 |
-2 |
1.5 |
1 |
6 |
| L= -18 |
Dj |
0 |
-2 |
0 |
-3 |
1 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={2,6}=2
Сделаем стобец x5 базисом.
К строке 2 прибавим строку 1.
К строке 3 прибавим (-3) строки 1.
Строку 1 умножим на 2.
Таблица11.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| -2 |
1 |
0 |
1 |
0 |
0 |
|
Bi/aij
|
| x5 |
2 |
0 |
0 |
-5 |
2 |
-2 |
1 |
0 |
|
| x1 |
10 |
-2 |
1 |
-2 |
1 |
0 |
0 |
0 |
|
| x6 |
6 |
0 |
0 |
8 |
-3 |
1 |
0 |
1 |
0.75 |
| L= -20 |
Dj |
0 |
3 |
-2 |
-1 |
0 |
0 |
|
Т.к. не все маргиналы меньше или равны нулю, то продолжаем оптимизацию.
min(Bi/aij)={0.75}=0.75
Сделаем стобец x2 базисом.
К строке 1 прибавим (0.625) строки 3.
К строке 2 прибавим (0.25) строки 3.
Строку 3 поделим на 8.
Таблица12.
| Xj0 |
B |
C |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
| -2 |
1 |
0 |
1 |
0 |
0 |
|
Bi/aij
|
| x5 |
5.75 |
0 |
0 |
0 |
0.125 |
-1.375 |
1 |
0.625 |
|
| x1 |
11.5 |
-2 |
1 |
0 |
0.25 |
0.25 |
0 |
0.25 |
|
| x2 |
0.75 |
1 |
0 |
1 |
-0.375 |
0.125 |
0 |
0.125 |
|
| L= -22.25 |
Dj |
0 |
0 |
-0.5 |
-1.5 |
0 |
-0.5 |
|
Все маргиналы меньше или равны нулю.
Оптимизация успешно завершена.
Найдено оптимальное решение:
Максимум:
X*=(11.5,0.75,0,0)T
L*= 22.25.
Ответ:
Минимум:
X*=(0,0,10,36)T
L*= -36.
Максимум:
X*=(11.5,0.75,0,0)T
L*= 22.25.
|


